Question
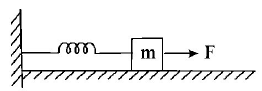
A block of mass $$m,$$ lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant $$k.$$ The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force $$F,$$ the maximum speed of the block is:
A block of mass $$m,$$ lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant $$k.$$ The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force $$F,$$ the maximum speed of the block is:
A.
$$\frac{{2F}}{{\sqrt {mk} }}$$
B.
$$\frac{F}{{\pi \sqrt {mk} }}$$
C.
$$\frac{{\pi F}}{{\sqrt {mk} }}$$
D.
$$\frac{F}{{\sqrt {mk} }}$$
Answer :
$$\frac{F}{{\sqrt {mk} }}$$
Solution :
Maximum speed is at equilibrium position where
$$F = kx \Rightarrow x = \frac{F}{k}$$
From work-energy theorem,
$$\eqalign{ & {W_F} + {W_{sp}} = \vartriangle KE \cr & F\left( x \right) - \frac{1}{2}k{x^2} = \frac{1}{2}m{v^2} - 0 \cr & F\left( {\frac{F}{k}} \right) - \frac{1}{2}k{\left( {\frac{F}{k}} \right)^2} = \frac{1}{2}m{v^2} \cr & \Rightarrow \frac{1}{2}\frac{{{F^2}}}{k} = \frac{1}{2}m{v^2} \cr & {\text{or,}}\,{v_{\max }} = \frac{F}{{\sqrt {mk} }} \cr} $$
Maximum speed is at equilibrium position where
$$F = kx \Rightarrow x = \frac{F}{k}$$
From work-energy theorem,
$$\eqalign{ & {W_F} + {W_{sp}} = \vartriangle KE \cr & F\left( x \right) - \frac{1}{2}k{x^2} = \frac{1}{2}m{v^2} - 0 \cr & F\left( {\frac{F}{k}} \right) - \frac{1}{2}k{\left( {\frac{F}{k}} \right)^2} = \frac{1}{2}m{v^2} \cr & \Rightarrow \frac{1}{2}\frac{{{F^2}}}{k} = \frac{1}{2}m{v^2} \cr & {\text{or,}}\,{v_{\max }} = \frac{F}{{\sqrt {mk} }} \cr} $$