Question
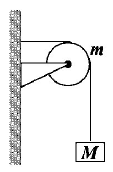
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle $$\theta $$ should be
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle $$\theta $$ should be

A.
$${0^ \circ }$$
B.
$${30^ \circ }$$
C.
$${45^ \circ }$$
D.
$${60^ \circ }$$
Answer :
$${45^ \circ }$$
Solution :
The tension in both strings will be same due to symmetry.

For equilibrium in vertical direction for body $$B$$ we have
$$\eqalign{ & \sqrt 2 \,mg = 2T\cos \theta \cr & \therefore \sqrt 2 \,mg = 2\left( {mg} \right)\cos \theta \,\left[ {\because T = mg,\,\left( {{\text{at}}\,{\text{equilibrium}}} \right.} \right] \cr & \therefore \cos \theta = \frac{1}{{\sqrt 2 }} \Rightarrow \theta = {45^ \circ } \cr} $$
The tension in both strings will be same due to symmetry.

For equilibrium in vertical direction for body $$B$$ we have
$$\eqalign{ & \sqrt 2 \,mg = 2T\cos \theta \cr & \therefore \sqrt 2 \,mg = 2\left( {mg} \right)\cos \theta \,\left[ {\because T = mg,\,\left( {{\text{at}}\,{\text{equilibrium}}} \right.} \right] \cr & \therefore \cos \theta = \frac{1}{{\sqrt 2 }} \Rightarrow \theta = {45^ \circ } \cr} $$