Question
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point $$O$$ on the ground is 45°. It flies off horizontally straight away from the point $$O.$$ After one second, the elevation of the bird from $$O$$ is reduced to 30°. Then the speed (in $$m/s$$ ) of the bird is
A.
$$20\sqrt 2 $$
B.
$$20\left( {\sqrt 3 - 1} \right)$$
C.
$$40\left( {\sqrt 2 - 1} \right)$$
D.
$$40\left( {\sqrt 3 - \sqrt 2 } \right)$$
Answer :
$$20\left( {\sqrt 3 - 1} \right)$$
Solution :
Let the speed be $$y\,\, m/sec.$$
Let $$AC$$ be the vertical pole of height $$20\, m.$$
Let $$O$$ be the point on the ground such that $$\angle \,AOC = {45^ \circ }$$
Let $$OC = x$$
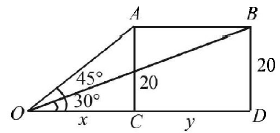
$$\eqalign{ & {\text{Time }}t = 1\,{\text{s}} \cr & {\text{From }}\Delta \,AOC,\tan {45^ \circ } = \frac{{20}}{x}\,\,\,\,\,.....\left( {\text{i}} \right) \cr & {\text{and from }}\Delta \,BOD,\tan {30^ \circ } = \frac{{20}}{{x + y}}\,\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
From (i) and (ii), we have $$x = 20\,\,{\text{and }}\frac{1}{{\sqrt 3 }} = \frac{{20}}{{x + y}}$$
$$\eqalign{ & \Rightarrow \,\,\frac{1}{{\sqrt 3 }} = \frac{{20}}{{20 + y}} \cr & \Rightarrow \,\,20 + y = 20\sqrt 3 \cr} $$
$${\text{So, }}y = 20\left( {\sqrt 3 - 1} \right)$$ i.e., speed $$ = 20\left( {\sqrt 3 - 1} \right){\text{m}}\,{\text{/s}}$$
Let the speed be $$y\,\, m/sec.$$
Let $$AC$$ be the vertical pole of height $$20\, m.$$
Let $$O$$ be the point on the ground such that $$\angle \,AOC = {45^ \circ }$$
Let $$OC = x$$

$$\eqalign{ & {\text{Time }}t = 1\,{\text{s}} \cr & {\text{From }}\Delta \,AOC,\tan {45^ \circ } = \frac{{20}}{x}\,\,\,\,\,.....\left( {\text{i}} \right) \cr & {\text{and from }}\Delta \,BOD,\tan {30^ \circ } = \frac{{20}}{{x + y}}\,\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
From (i) and (ii), we have $$x = 20\,\,{\text{and }}\frac{1}{{\sqrt 3 }} = \frac{{20}}{{x + y}}$$
$$\eqalign{ & \Rightarrow \,\,\frac{1}{{\sqrt 3 }} = \frac{{20}}{{20 + y}} \cr & \Rightarrow \,\,20 + y = 20\sqrt 3 \cr} $$
$${\text{So, }}y = 20\left( {\sqrt 3 - 1} \right)$$ i.e., speed $$ = 20\left( {\sqrt 3 - 1} \right){\text{m}}\,{\text{/s}}$$