Question
A balloon starts rising from the surface of the earth. The ascension rate is constant and equal to $${v_0}.$$ Due to the wind the balloon gathered the horizontal velocity component $${v_x} = ay,$$ where $$a$$ is a constant and $$y$$ is the height of ascent. The tangential, acceleration of the balloon is
A.
$$\frac{{{a^2}y}}{{{v_0}}}$$
B.
$$\frac{{{a^2}y}}{{\sqrt {1 + {{\left( {\frac{{{a^2}y}}{{{v_0}}}} \right)}^2}} }}$$
C.
$$\frac{{{a^2}y}}{{\sqrt {1 + v_0^2} }}$$
D.
$$\frac{{{a^2}{v_0}}}{{\sqrt {1 + {{\left( {\frac{{2y}}{a}} \right)}^2}} }}$$
Answer :
$$\frac{{{a^2}y}}{{\sqrt {1 + {{\left( {\frac{{{a^2}y}}{{{v_0}}}} \right)}^2}} }}$$
Solution :
Since velocity in vertical direction is constant,
$$\therefore {a_y} = \frac{{d{v_y}}}{{dt}} = 0$$
The acceleration in horizontal direction,
$$\eqalign{ & {a_x} = \frac{{d{v_x}}}{{dt}} = \frac{{d\left( {a{v_0}t} \right)}}{{dt}} = a{v_0} \cr & a = \sqrt {a_x^2 + a_y^2} = \sqrt {{{\left( {a{v_0}} \right)}^2} + 0} = a{v_0} \cr} $$
The total acceleration is $$a{v_0}$$ and directed along horizontal direction.
Let $$\theta $$ is the angle that the resultant velocity makes with horizontal, then
Normal acceleration $${a_n} = a\sin \theta $$ and tangential acceleration
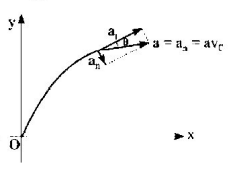
$$\eqalign{ & {a_t} = a\cos \theta ,\,{\text{we}}\,{\text{have}}\,x = \frac{{a{y^2}}}{{2{v_0}}} \cr & {\text{or}}\,\,y = \sqrt {\frac{{2x{v_0}}}{a}} \cr} $$
Differentiating both side of equation (iii) w.r.t. $$x,$$ we get
$$1 = \frac{a}{{2{v_0}}} \times 2y \times \frac{{dy}}{{dx}}$$
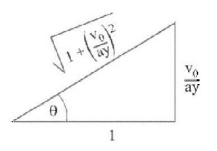
$$\eqalign{ & {\text{or}}\,\,\frac{{dy}}{{dx}} = \frac{{{v_0}}}{{ay}} = \tan \theta \cr & {\text{Now}}\,\,{a_x} = a\sin \theta = a{v_0} \times \frac{{\left( {\frac{{{v_0}}}{{ay}}} \right)}}{{\sqrt {1 + {{\left( {\frac{{{v_0}}}{{ay}}} \right)}^2}} }} \cr & = \frac{{a{v_0}}}{{\sqrt {1 + {{\left( {\frac{{ay}}{{{v_0}}}} \right)}^2}} }} \cr & {a_t} = a\cos \theta = a{v_0} \times \frac{1}{{\sqrt {1 + {{\left( {\frac{{{v_0}}}{{ay}}} \right)}^2}} }} = a{v_0} \cr & \frac{{ay}}{{\sqrt {{{\left( {ay} \right)}^2} + v_0^2} }} = \frac{{{a^2}y}}{{\sqrt {1 + {{\left( {\frac{{ay}}{{{v_0}}}} \right)}^2}} }} \cr} $$
Since velocity in vertical direction is constant,
$$\therefore {a_y} = \frac{{d{v_y}}}{{dt}} = 0$$
The acceleration in horizontal direction,
$$\eqalign{ & {a_x} = \frac{{d{v_x}}}{{dt}} = \frac{{d\left( {a{v_0}t} \right)}}{{dt}} = a{v_0} \cr & a = \sqrt {a_x^2 + a_y^2} = \sqrt {{{\left( {a{v_0}} \right)}^2} + 0} = a{v_0} \cr} $$
The total acceleration is $$a{v_0}$$ and directed along horizontal direction.
Let $$\theta $$ is the angle that the resultant velocity makes with horizontal, then
Normal acceleration $${a_n} = a\sin \theta $$ and tangential acceleration

$$\eqalign{ & {a_t} = a\cos \theta ,\,{\text{we}}\,{\text{have}}\,x = \frac{{a{y^2}}}{{2{v_0}}} \cr & {\text{or}}\,\,y = \sqrt {\frac{{2x{v_0}}}{a}} \cr} $$
Differentiating both side of equation (iii) w.r.t. $$x,$$ we get
$$1 = \frac{a}{{2{v_0}}} \times 2y \times \frac{{dy}}{{dx}}$$

$$\eqalign{ & {\text{or}}\,\,\frac{{dy}}{{dx}} = \frac{{{v_0}}}{{ay}} = \tan \theta \cr & {\text{Now}}\,\,{a_x} = a\sin \theta = a{v_0} \times \frac{{\left( {\frac{{{v_0}}}{{ay}}} \right)}}{{\sqrt {1 + {{\left( {\frac{{{v_0}}}{{ay}}} \right)}^2}} }} \cr & = \frac{{a{v_0}}}{{\sqrt {1 + {{\left( {\frac{{ay}}{{{v_0}}}} \right)}^2}} }} \cr & {a_t} = a\cos \theta = a{v_0} \times \frac{1}{{\sqrt {1 + {{\left( {\frac{{{v_0}}}{{ay}}} \right)}^2}} }} = a{v_0} \cr & \frac{{ay}}{{\sqrt {{{\left( {ay} \right)}^2} + v_0^2} }} = \frac{{{a^2}y}}{{\sqrt {1 + {{\left( {\frac{{ay}}{{{v_0}}}} \right)}^2}} }} \cr} $$




