Question
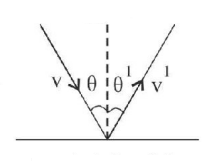
A ball of mass $$m$$ hits the floor making an angle $$\theta $$ as shown in the figure. If $$e$$ is the coefficient of restitution, then which relation is true, for the velocity component before and after collision?
A ball of mass $$m$$ hits the floor making an angle $$\theta $$ as shown in the figure. If $$e$$ is the coefficient of restitution, then which relation is true, for the velocity component before and after collision?
A.
$${V^1}\sin \theta ' = V\sin \theta $$
B.
$${V^1}\sin \theta ' = - \sin \theta $$
C.
$${V^1}\cos \theta ' = V\cos \theta $$
D.
$${V^1}\cos \theta ' = - V\cos \theta $$
Answer :
$${V^1}\sin \theta ' = V\sin \theta $$
Solution :
As the floor exerts a force on the ball along the normal, & no force parallel to the surface, therefore the velocity component along the parallel to the floor remains constant.
Hence $$V\sin \theta = {V^1}\sin {\theta ^1}$$
As the floor exerts a force on the ball along the normal, & no force parallel to the surface, therefore the velocity component along the parallel to the floor remains constant.
Hence $$V\sin \theta = {V^1}\sin {\theta ^1}$$