Question
A ball is dropped from the top of a tower of height $$100\,m$$ and at the same time another ball is projected vertically upwards from ground with a velocity $$25\,m{s^{ - 1}}.$$ Then the distance from the top of the tower, at which the two balls meet is
A.
$$68.4\,m$$
B.
$$48.4\,m$$
C.
$$18.4\,m$$
D.
$$78.4\,m$$
Answer :
$$78.4\,m$$
Solution :
Let the two balls $$P$$ and $$Q$$ meet at height $$x$$ $$m$$ from the ground after time $$ts$$ from the start. We have to find distance, $$BC = \left( {100 - x} \right)$$
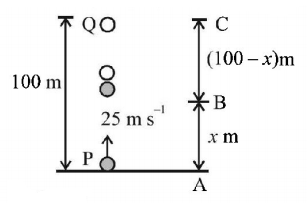
For ball $$P$$
$$\eqalign{ & S = xm,u = 25\;m{s^{ - 1}},a = - g \cr & {\text{From}}\,\,S = ut + \frac{1}{2}a{t^2} \cr & x = 25t - \frac{1}{2}g{t^2}\,......\left( {\text{i}} \right) \cr} $$
For ball $$Q$$
$$\eqalign{ & S = \left( {100 - x} \right)m,u = 0,a = g \cr & \therefore 100 - x = 0 + \frac{1}{2}g{t^2}\,......\left( {{\text{ii}}} \right) \cr} $$
Adding eqns. (i) and (ii), we get
$$100 = 25t\,\,{\text{or}}\,\,t = 4\,s$$
From eqn. (i),
$$x = 25 \times 4 - \frac{1}{2} \times 9.8 \times {\left( 4 \right)^2} = 21.6\,m$$
Hence distance from the top of the tower
$$ = \left( {100 - x} \right)m = \left( {100 - 21.6\,m} \right) = 78.4\,m$$
Let the two balls $$P$$ and $$Q$$ meet at height $$x$$ $$m$$ from the ground after time $$ts$$ from the start. We have to find distance, $$BC = \left( {100 - x} \right)$$

For ball $$P$$
$$\eqalign{ & S = xm,u = 25\;m{s^{ - 1}},a = - g \cr & {\text{From}}\,\,S = ut + \frac{1}{2}a{t^2} \cr & x = 25t - \frac{1}{2}g{t^2}\,......\left( {\text{i}} \right) \cr} $$
For ball $$Q$$
$$\eqalign{ & S = \left( {100 - x} \right)m,u = 0,a = g \cr & \therefore 100 - x = 0 + \frac{1}{2}g{t^2}\,......\left( {{\text{ii}}} \right) \cr} $$
Adding eqns. (i) and (ii), we get
$$100 = 25t\,\,{\text{or}}\,\,t = 4\,s$$
From eqn. (i),
$$x = 25 \times 4 - \frac{1}{2} \times 9.8 \times {\left( 4 \right)^2} = 21.6\,m$$
Hence distance from the top of the tower
$$ = \left( {100 - x} \right)m = \left( {100 - 21.6\,m} \right) = 78.4\,m$$




