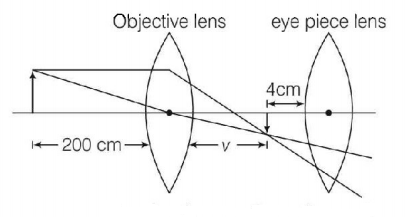
A astronomical telescope has objective and eyepiece of focal lengths $$40\,cm$$  $$4\,cm$$  respectively. To view an object $$200\,cm$$  away from the objective, the lenses must be separated by a distance

Solution :
According to question,
Focal length of objective lens $$\left( {{F_0}} \right) = + 40\,cm$$
Focal length of eyepiece lens $$\left( {{F_e}} \right) = 4\,cm$$
Object distance for objective lens $$\left( {{u_0}} \right) = - 200\,cm$$
Applying lens formula for objective lens

$$\eqalign{ & \frac{1}{v} - \frac{1}{u} = \frac{1}{f} \Rightarrow \frac{1}{v} - \frac{1}{{ - 200}} = \frac{1}{{40}} \cr & \Rightarrow \frac{1}{v} = \frac{1}{{40}} - \frac{1}{{200}} = \frac{{5 - 1}}{{200}} = \frac{4}{{200}} \cr & \Rightarrow v = 50\,cm \cr} $$
Image will be form at first focus of eyepiece lens. So, for normal adjustment distance between objectives and eye piece lense (length of tube) will be
$$v + {F_e} \Rightarrow 50 + 4 \Rightarrow 54\,cm$$