Question
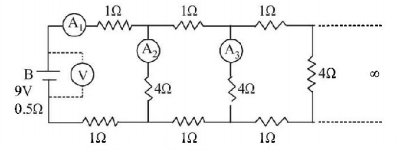
A $$9\,V$$ battery with internal resistance of $$0.5\,\Omega $$ is connected across an infinite network as shown in the figure. All ammeters $${A_1},{A_2},{A_3}$$ and voltmeter $$V$$ are ideal.
Choose correct statement.
A.
Reading of $${A_1}$$ is $$2\,A$$
B.
Reading of $${A_1}$$ is $$18\,A$$
C.
Reading of $$V$$ is $$9\,V$$
D.
Reading of $$V$$ is $$7\,V$$
Answer :
Reading of $${A_1}$$ is $$2\,A$$
Solution :
The given circuit can be redrawn as,
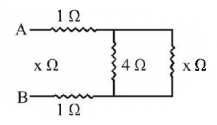
as $$4\,\Omega $$ and $$x\,\Omega $$ are parallel
$$\eqalign{ & x' = \frac{1}{4} + \frac{1}{x} = \frac{{\left( {4 + x} \right)}}{{4x}} \cr & x' = \frac{{4x}}{{4 + x}} \cr} $$
$$\& 1\,\Omega $$ and $$1\,\Omega $$ are also parallel $$x'' = 2\,\Omega $$
Now equivalent resistance of circuit
$$\eqalign{ & x = \frac{{4x}}{{4 + x}} + 2 = \frac{{8 + 6x}}{{4 + x}} \cr & 4x + {x^2} = 8 + 6x \cr & \Rightarrow {x^2} - 2x - 8 = 0 \cr & x = \frac{{2 \pm \sqrt {4 - 4\left( 1 \right)\left( { - 8} \right)} }}{2} \cr & = \frac{{2 \pm \sqrt {36} }}{2} = 4\Omega \cr} $$
Reading of Ammeter $${A_1} = \frac{V}{{\left( {R + r} \right)}}$$
$${A_1} = \frac{9}{{4 + 0.5}} = 2\,{\text{Ampere}}$$
The given circuit can be redrawn as,

as $$4\,\Omega $$ and $$x\,\Omega $$ are parallel
$$\eqalign{ & x' = \frac{1}{4} + \frac{1}{x} = \frac{{\left( {4 + x} \right)}}{{4x}} \cr & x' = \frac{{4x}}{{4 + x}} \cr} $$
$$\& 1\,\Omega $$ and $$1\,\Omega $$ are also parallel $$x'' = 2\,\Omega $$
Now equivalent resistance of circuit
$$\eqalign{ & x = \frac{{4x}}{{4 + x}} + 2 = \frac{{8 + 6x}}{{4 + x}} \cr & 4x + {x^2} = 8 + 6x \cr & \Rightarrow {x^2} - 2x - 8 = 0 \cr & x = \frac{{2 \pm \sqrt {4 - 4\left( 1 \right)\left( { - 8} \right)} }}{2} \cr & = \frac{{2 \pm \sqrt {36} }}{2} = 4\Omega \cr} $$
Reading of Ammeter $${A_1} = \frac{V}{{\left( {R + r} \right)}}$$
$${A_1} = \frac{9}{{4 + 0.5}} = 2\,{\text{Ampere}}$$
