A $$2\,m$$  wide truck is moving with a uniform speed $${v_0} = 8\,m/s$$   along a straight horizontal road. A pedestrain starts to cross the road with a uniform speed $$v$$ when the truck is $$4m$$  away from him. The minimum value of $$v$$ so that he can cross the road safely is

Solution :
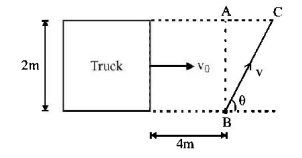
Let the man starts crossing the road at an angle $$\theta $$ as shown in figure. For safe crossing the condition is that the man must cross the road by the time the truck describes the distance $$4 + AC$$  or $$4 + 2\cot \theta .$$
$$\therefore \frac{{4 + 2\cot \theta }}{8} = \frac{{\frac{2}{{\sin \theta }}}}{v}\,\,{\text{or}}\,\,v = \frac{8}{{2\sin \theta + \cos \theta }}\,......\left( {\text{i}} \right)$$
For minimum $$v,\frac{{dv}}{{d\theta }} = 0$$

$$\eqalign{ & {\text{or}}\,\,\frac{{ - 8\left( {2\cos \theta - \sin \theta } \right)}}{{\left( {2\cos \theta + \sin \theta } \right)}} = 0 \cr & {\text{or}}\,2\cos \theta - \sin \theta = 0\,\,{\text{or}}\,\,\tan \theta = 2 \cr} $$
From equation (i),
$${v_{\min }} = \frac{8}{{2\left( {\frac{2}{{\sqrt 5 }}} \right) + \frac{1}{{\sqrt 5 }}}} = \frac{8}{{\sqrt 5 }} = 3.57\,m/s$$