Question
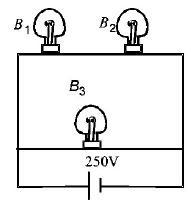
A $$100\,W$$ bulb $${B_1}$$ and two $$60\,W$$ bulb $${B_2}$$ and $${B_3},$$ are connected to a $$250\,V$$ source, as shown in figure. Now $${W_1},{W_2}$$ and $${W_3}$$ are the output powers of the bulbs $${B_1},{B_2}$$ and $${B_3},$$ respectively. Then
A $$100\,W$$ bulb $${B_1}$$ and two $$60\,W$$ bulb $${B_2}$$ and $${B_3},$$ are connected to a $$250\,V$$ source, as shown in figure. Now $${W_1},{W_2}$$ and $${W_3}$$ are the output powers of the bulbs $${B_1},{B_2}$$ and $${B_3},$$ respectively. Then
A.
$${W_1} > {W_2} = {W_3}$$
B.
$${W_1} > {W_2} > {W_3}$$
C.
$${W_1} < {W_2} = {W_3}$$
D.
$${W_1} < {W_2} < {W_3}$$
Answer :
$${W_1} < {W_2} < {W_3}$$
Solution :
KEY CONCEPT : $$R = \frac{{{V^2}}}{P}$$
$$\therefore {R_1} = \frac{{{V^2}}}{{100}},{R_2} = \frac{{{V^2}}}{{60}} = {R_3};$$
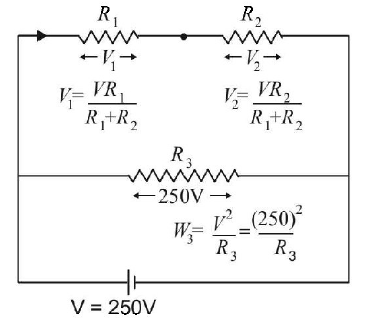
$$\eqalign{ & {W_1} = \frac{{V_1^2}}{{{R_1}}} = \frac{{{V^2}{R_1}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}},\,{W_2} = \frac{{V_2^2}}{{{R_2}}} = \frac{{{V^2}{R_2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}} \cr & {\text{and }}{W_3} = \frac{{{V^2}}}{{{R_3}}} \cr & {W_3}:{W_2}:{W_1} = \frac{{{{\left( {250} \right)}^2}}}{{{R_3}}}:\frac{{{{\left( {250} \right)}^2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}}{R_2}:\frac{{{{\left( {250} \right)}^2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}}{R_1} \cr & {\text{or }}{W_3}:{W_2}:{W_1} = \frac{{{{\left( {250} \right)}^2}}}{{{V^2}}} \times 60:\frac{{{{\left( {250} \right)}^2}}}{{{{\left[ {\frac{1}{{100}} + \frac{1}{{60}}} \right]}^2}{V^4}}} \times \frac{{{V^2}}}{{60}}:\frac{{{{\left( {250} \right)}^2}{V^2}}}{{{{\left[ {\frac{1}{{100}} + \frac{1}{{60}}} \right]}^2}{V^4} \times 1000}} \cr & {\text{or }}{W_3}:{W_2}:{W_1} = 60:\frac{{100 \times 100 \times 60 \times 60}}{{160 \times 160 \times 60}}:\frac{{100 \times 100 \times 60 \times 60}}{{160 \times 160 \times 100}} \cr & = 64:25:15 \cr} $$
KEY CONCEPT : $$R = \frac{{{V^2}}}{P}$$
$$\therefore {R_1} = \frac{{{V^2}}}{{100}},{R_2} = \frac{{{V^2}}}{{60}} = {R_3};$$

$$\eqalign{ & {W_1} = \frac{{V_1^2}}{{{R_1}}} = \frac{{{V^2}{R_1}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}},\,{W_2} = \frac{{V_2^2}}{{{R_2}}} = \frac{{{V^2}{R_2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}} \cr & {\text{and }}{W_3} = \frac{{{V^2}}}{{{R_3}}} \cr & {W_3}:{W_2}:{W_1} = \frac{{{{\left( {250} \right)}^2}}}{{{R_3}}}:\frac{{{{\left( {250} \right)}^2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}}{R_2}:\frac{{{{\left( {250} \right)}^2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}}{R_1} \cr & {\text{or }}{W_3}:{W_2}:{W_1} = \frac{{{{\left( {250} \right)}^2}}}{{{V^2}}} \times 60:\frac{{{{\left( {250} \right)}^2}}}{{{{\left[ {\frac{1}{{100}} + \frac{1}{{60}}} \right]}^2}{V^4}}} \times \frac{{{V^2}}}{{60}}:\frac{{{{\left( {250} \right)}^2}{V^2}}}{{{{\left[ {\frac{1}{{100}} + \frac{1}{{60}}} \right]}^2}{V^4} \times 1000}} \cr & {\text{or }}{W_3}:{W_2}:{W_1} = 60:\frac{{100 \times 100 \times 60 \times 60}}{{160 \times 160 \times 60}}:\frac{{100 \times 100 \times 60 \times 60}}{{160 \times 160 \times 100}} \cr & = 64:25:15 \cr} $$
