Question
$$1\,kg$$ body explodes into three fragments. The ratio of their masses is $$1:1:3.$$ The fragments of same mass move perpendicular to each other with speeds $$30\,m/s,$$ while the heavier part remains in the initial direction. The speed of heavier part is
A.
$$\frac{{10}}{{\sqrt 2 }}m/s$$
B.
$$10\sqrt 2 \,m/s$$
C.
$$20\sqrt 2 \,m/s$$
D.
$$30\sqrt 2 \,m/s$$
Answer :
$$10\sqrt 2 \,m/s$$
Solution :
Apply conservation of momentum with direction.
Let $$u$$ be the velocity and $$\theta $$ the direction of the third piece as shown.
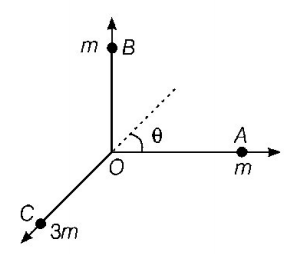
Equating the momentum of the system along $$OA$$ and $$OB$$ to zero, we get
$$\eqalign{ & m \times 30 - 3m \times v\cos \theta = 0\,......\left( {\text{i}} \right) \cr & {\text{and}}\,m \times 30 - 3m \times v\sin \theta = 0\,......\left( {{\text{ii}}} \right) \cr} $$
From Eqs. (i) and (ii), we get
$$\eqalign{ & 3mv\cos \theta = 3mv\sin \theta \cr & {\text{or}}\,\,\cos \theta = \sin \theta \cr & \therefore \theta = {45^ \circ } \cr & {\text{Thus,}}\,\,\angle AOC = \angle BOC \cr & = {180^ \circ } - {45^ \circ } = {135^ \circ } \cr} $$
Putting the value of $$\theta $$ in Eq. (i), we get
$$\eqalign{ & 30\;m = 3\;mv\cos {45^ \circ } = \frac{{3mv}}{{\sqrt 2 }} \cr & \therefore v = 10\sqrt 2 \,m/s \cr} $$
The third piece will go with a velocity of $$10\sqrt 2 \,m/s$$ in a direction making an angle of $${135^ \circ }$$ with either piece.
Alternative
The square of momentum of third piece is equal to sum of squares of momentum first and second pieces.
$$\eqalign{ & p_3^2 = p_1^2 + p_2^2 \cr & {\text{or}}\,\,{p_3} = \sqrt {p_1^2 + p_2^2} \cr & {\text{or}}\,\,3m{v_3} = \sqrt {{{\left( {m \times 30} \right)}^2} + {{\left( {m \times 30} \right)}^2}} \cr & {\text{or}}\,\,{v_3} = \frac{{30\sqrt 2 }}{3} \cr & = 10\sqrt 2 \,m/s \cr} $$
Apply conservation of momentum with direction.
Let $$u$$ be the velocity and $$\theta $$ the direction of the third piece as shown.

Equating the momentum of the system along $$OA$$ and $$OB$$ to zero, we get
$$\eqalign{ & m \times 30 - 3m \times v\cos \theta = 0\,......\left( {\text{i}} \right) \cr & {\text{and}}\,m \times 30 - 3m \times v\sin \theta = 0\,......\left( {{\text{ii}}} \right) \cr} $$
From Eqs. (i) and (ii), we get
$$\eqalign{ & 3mv\cos \theta = 3mv\sin \theta \cr & {\text{or}}\,\,\cos \theta = \sin \theta \cr & \therefore \theta = {45^ \circ } \cr & {\text{Thus,}}\,\,\angle AOC = \angle BOC \cr & = {180^ \circ } - {45^ \circ } = {135^ \circ } \cr} $$
Putting the value of $$\theta $$ in Eq. (i), we get
$$\eqalign{ & 30\;m = 3\;mv\cos {45^ \circ } = \frac{{3mv}}{{\sqrt 2 }} \cr & \therefore v = 10\sqrt 2 \,m/s \cr} $$
The third piece will go with a velocity of $$10\sqrt 2 \,m/s$$ in a direction making an angle of $${135^ \circ }$$ with either piece.
Alternative
The square of momentum of third piece is equal to sum of squares of momentum first and second pieces.
$$\eqalign{ & p_3^2 = p_1^2 + p_2^2 \cr & {\text{or}}\,\,{p_3} = \sqrt {p_1^2 + p_2^2} \cr & {\text{or}}\,\,3m{v_3} = \sqrt {{{\left( {m \times 30} \right)}^2} + {{\left( {m \times 30} \right)}^2}} \cr & {\text{or}}\,\,{v_3} = \frac{{30\sqrt 2 }}{3} \cr & = 10\sqrt 2 \,m/s \cr} $$
